Computational Science

Computational science is an interdisciplinary field that uses mathematical models, algorithms, and computer simulations to study and solve complex scientific and engineering problems. It stands at the intersection of mathematics, computer science, and domain-specific sciences (like physics, biology, chemistry, or economics).

How Living Things Stay “Themselves” (Even When Everything Inside Changes)

~ Manuel Castañón-Puga

You know that weird moment when you’ve had a rough week, skipped sleep, eaten random snacks, and still wake up feeling like… you’re still you? The paper by Varela, Maturana, and Uribe digs into that everyday mystery from a very grounded angle: not “what are living things made of?”, but “what kind of ongoing pattern makes something a living unit at all?” Their starting point is that focusing only on parts can miss what actually matters: the organization that makes the whole hold together as one distinct “someone” or “something,” whether or not it’s reproducing.

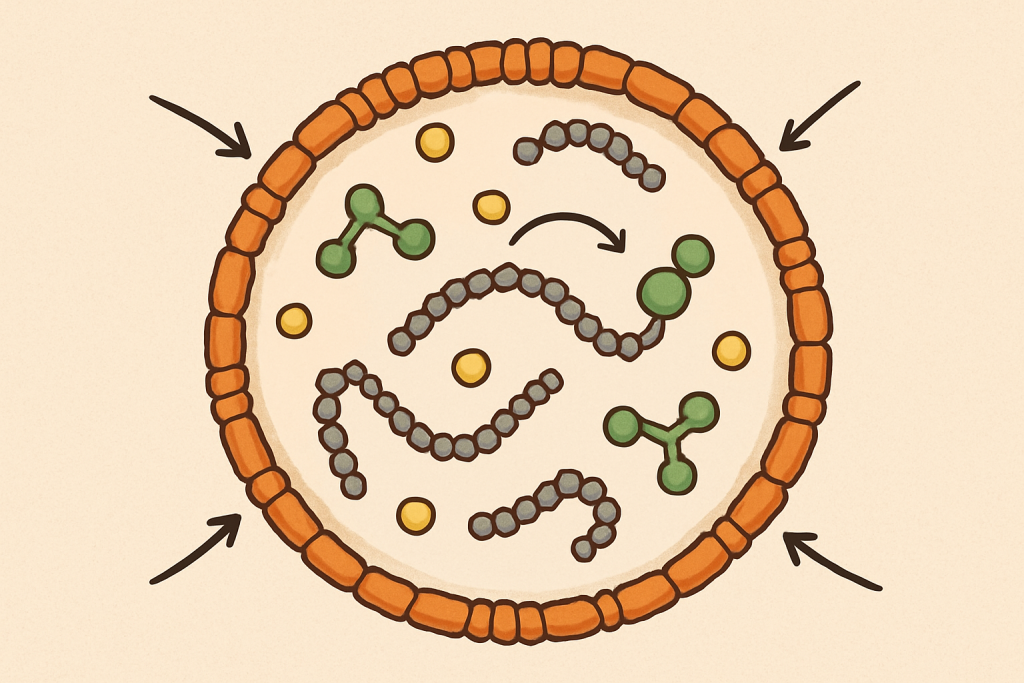
Their key idea is called autopoiesis, which basically means “self-making.” A living system, in their description, is a network of processes that continually produces the very components that sustain the network. At the same time, it builds and maintains a boundary that makes it a recognizable unit in its space. They use the cell as the easy example: a vast web of chemical reactions keeps making molecules that keep those reactions possible, and together those molecules keep the cell as a physical, separate “thing,” even though the actual matter inside is constantly being replaced. In that picture, what makes something alive is not a specific ingredient, but a looping, self-maintaining organization. That’s also why they contrast living systems with allopoietic ones: many machines produce something other than themselves, while an autopoietic system’s “output” is basically its own continued existence as that same kind of unity.

This also changes the way we think about reproduction. The authors argue that reproduction and evolution are essential. Still, they aren’t the basic definition of being alive, because you can’t reproduce unless you already have a living unity to reproduce in the first place. In their view, reproduction happens as a special case of this self-maintaining organization: the unit can split so that the same kind of self-producing network continues in two fragments. To make the idea less abstract, they present a minimal computer model in a simple grid-world: elements bump around randomly, a “catalyst” helps create “links,” and links bond into chains. Sometimes a chain closes into a loop that traps the catalyst inside. Once that happens, new links formed inside can replace boundary links that fall apart. Hence, the boundary stays intact even though parts keep turning over—like fixing a fence plank-by-plank without ever letting the yard stop being enclosed. They even give a practical “checklist” style key (six points) for deciding if something counts as autopoietic: can you find a boundary, identify components, see a rule-governed system, confirm the boundary is produced by interactions of elements, and confirm the components (including boundary ones) are continually made and participate in creating others.

The everyday takeaway is surprisingly useful: it’s a reminder to look for the pattern that keeps something going, not just the content itself. Your body, habits, relationships, even a group project, can “feel alive” or “fall apart” depending on whether the ongoing loop that sustains it is still running—and whether there’s a boundary that protects that loop from getting wrecked by every outside bump. In the paper, when the network of production breaks, the unity disintegrates; when it can compensate for disturbances, it stays autonomous. That’s a simple lens you can apply day-to-day: if you want a system (you, a routine, a shared apartment, a club) to stay stable while everything changes, focus on the repeating actions that rebuild the structure and the boundary conditions that make those actions possible. The authors even point toward how this thinking could guide attempts to build “life-like” systems in chemistry, like imagining a bubble-like structure whose membrane components are produced or modified by reactions that happen within the special conditions created by the membrane itself—because what matters most is not the material, but the self-maintaining loop that makes a unit a unit.

Reference:
Varela, F. G., Maturana, H. R., & Uribe, R. (1974). Autopoiesis: The organization of living systems, its characterization and a model. Biosystems, 5(4), 187–196. https://doi.org/10.1016/0303-2647(74)90031-8

Privacy Notice & Disclaimer:
This blog provides simplified educational science content, created with the assistance of both humans and AI. It may omit technical details, is provided “as is,” and does not collect personal data beyond basic anonymous analytics. For full details, please see our Privacy Notice and Disclaimer. Read About This Blog & Attribution Note for AI-Generated Content to know more about this blog project.

How Simple Rules Can Create Surprising Worlds

~ Manuel Castañón-Puga

Imagine you’re doodling on squared paper during a long bus ride. You start by coloring a few squares randomly. Then you make up a rule: “If a square has two colored neighbors, color it next turn; otherwise leave it blank.” You move to the next row, applying the rule repeatedly. At first, it feels like nothing special. But suddenly, shapes appear—lines, triangles, even messy bursts that seem almost alive. That moment when order emerges from randomness feels magical, yet it follows from just a few simple steps.

According to Stephen Wolfram, whose work explores the hidden patterns behind these kinds of drawings—called cellular automata—this magic isn’t accidental. He explains that even elementary rules, when repeated repeatedly, can create four distinct “personalities” of behavior. Some rules calm everything down until all squares look the same. Others make small, repeating shapes that move or remain stationary. Some explode into chaos, filling the page with unpredictability. And a few very special rules mix order and chaos in a way so rich that they can even perform a kind of computation, similar to how a computer processes information.

To picture this, imagine baking cookies with four different cookie doughs. One dough always flattens into a smooth cookie, no matter what shape you start with—that’s like the rule that makes everything look uniform. Another dough always forms neat little bumps or rings—that’s the rule that creates simple repeating structures. A third dough spreads unpredictably, making patterns that never look the same twice—this is the chaotic dough. And finally, the fourth dough sometimes forms bumps, sometimes remains flat, and sometimes creates complex patterns that resemble miniature machines. Wolfram shows that this last type is potent because its results can’t be predicted without actually going step by step, just like running a program.

What makes this useful for everyday life is realizing how often simple rules create complex outcomes. Imagine a group chat where one person responds to a message, and then others react to that response. A tiny interaction can ripple outward and shape the whole conversation. Or think of routines: hitting “snooze” once might seem harmless, but repeated daily, it shapes your whole morning rhythm. Small rules, repeated over time, add up. Wolfram’s point is that complexity doesn’t always come from complicated instructions—it often comes from elementary ones applied consistently.

It’s also a reminder that not everything can be predicted just by analyzing the rules. Some processes (such as how ideas spread online, how habits form, or how friend groups evolve) can only be understood by observing them unfold. Wolfram’s fourth type of behavior teaches us that even if we know all the rules, we might still need to observe change step by step. That’s not a limitation—it’s an invitation to explore, experiment, and stay curious about the patterns that shape our daily lives.

Reference:
Wolfram, S. (1984). Universality and complexity in cellular automata. Physica D: Nonlinear Phenomena, 10(1–2), 1–35. https://doi.org/10.1016/0167-2789(84)90245-8

Privacy Notice & Disclaimer:
This blog provides simplified educational science content, created with the assistance of both humans and AI. It may omit technical details, is provided “as is,” and does not collect personal data beyond basic anonymous analytics. For full details, please see our Privacy Notice and Disclaimer. Read About This Blog & Attribution Note for AI-Generated Content to know more about this blog project.

When Your Model Isn’t Big Enough: How We Learn to See Hidden Patterns

~ Manuel Castañón-Puga

Picture you trying to make sense of a messy playlist. At first, you just note each song. Soon, you group them by mood. Then you realize there’s a deeper rule: the same three vibes always cycle, just in different lengths. You didn’t change the music. You changed how you looked at it. James P. Crutchfield describes this shift as “innovation” in how we model the world. When our current way of organizing data runs out of steam, we jump to a new, more capable way of seeing cause and effect. That jump, not more data alone, is what reveals the structure that felt like noise a moment ago.

Crutchfield’s method, called hierarchical ε-machine reconstruction, climbs a ladder of models, starting with the raw stream, then moving to trees, and finally to finite automata, and, if necessary, to richer machines. Try the simplest class first; if the model continues to grow as you feed it more data, that’s your cue to “innovate” and move up a level. The goal is the smallest model at the least powerful level that still captures the regularities, because small, right-sized models predict best. Think of it like upgrading from sorting songs one by one to folders, to smart playlists that automatically recognize patterns. The process continues until your model remains finite and predictive.

When should you upgrade? Crutchfield offers a simple rule of thumb: innovate once your model’s size reaches the point where it pushes against your own capacity. He even defines an “innovation rate” to identify when complexity is escalating as you refine the fit. If you ignore that signal, you’ll mistake lawful structure for random chatter. Real examples make this vivid. At the edge of chaos in a classic system, a naive model explodes into infinitely many states; the fix is to innovate a new representation that uses a stack-like memory, turning the “infinite” into a tidy finite description. And sometimes the opposite lesson hits: use the wrong instrument, and even a simple world looks impossibly complex. The remedy is to innovate the sensor model itself—say, by adding a counter that tracks how long you’ve seen the same symbol—so your description shrinks back to size.

Why does this matter day to day? Because we all model. Studying, budgeting, training, even scrolling—each is a guess about “what comes next.” Crutchfield shows that progress comes from knowing when to keep it simple and when to change the game. If your study notes become bloated without boosting recall, consider switching from lists to concept maps. If your workout tracker can’t spot plateaus, add a new feature like moving averages—a small “counter” that changes what you can see. If a chaotic group chat looks unreadable, filter for themes—your “domain and particle” view—to reveal structure under the noise. The big idea is practical: organize your limited attention into smarter models and be ready to innovate when your current one reaches its limits. That’s how hidden order shows up, prediction improves, and “random” turns into patterns you can actually use.

Reference:
Crutchfield, J. P. (1994). The calculi of emergence: computation, dynamics and induction. Physica D: Nonlinear Phenomena, 75(1–3), 11–54. https://doi.org/10.1016/0167-2789(94)90273-9

Privacy Notice & Disclaimer:
This blog provides simplified educational science content, created with the assistance of both humans and AI. It may omit technical details, is provided “as is,” and does not collect personal data beyond basic anonymous analytics. For full details, please see our Privacy Notice and Disclaimer. Read About This Blog & Attribution Note for AI-Generated Content to know more about this blog project.

Seeing Hidden Order in a Noisy World

~ Manuel Castañón-Puga

You’re scrolling through your phone, jumping from texts to videos to homework. Some things feel random. Some things feel predictable. Yet you still try to guess what comes next — the plot twist, the next notification, the teacher’s quiz question. Crutchfield argues that this everyday guessing game mirrors how scientists build models: they try to capture the useful patterns and treat the rest as “noise,” balancing simple explanations with good predictions instead of chasing either alone. In practice, the “best” model is the one that minimizes both the model’s size and the leftover randomness.

According to Crutchfield, what makes something truly interesting isn’t just pure order or pure randomness, but the mix in between. He describes “statistical complexity,” a method for measuring the amount of structure a process possesses. Purely random and perfectly periodic signals are actually simple by this measure; the richest structure lives between those extremes, where predictable and unpredictable pieces interact. Imagine a playlist that’s not totally shuffled and not a loop — it feels “designed” because it has memory and variation. That’s where complexity peaks.

Here’s the twist that helps in real life: systems can create patterns that the system itself then uses. Crutchfield calls this “intrinsic emergence.” Think of prices in a marketplace or trending topics online. They don’t come from one boss; they emerge from everyone’s actions and then guide what everyone does next. In this view, something “emerges” when the way information is processed changes — when the system gains new internal capability, not just a new look from the outside. That’s different from simply spotting a pretty pattern after the fact.

So, how do we improve at spotting and utilizing structure? Crutchfield’s answer is to build the simplest model that still predicts well, then upgrade only when the current approach continues to grow without limit. His framework, based on reconstructing minimal “machines,” treats model size as the memory you need to make good forecasts; when your model bloats, you “innovate” to a new class that captures the pattern more cleanly. In everyday terms: don’t memorize every detail of a course, a habit, or a feed; learn the few states that actually matter for predicting what comes next — and when that stops working, change how you’re thinking, not just how much you’re cramming.

Reference:
Crutchfield, J. P. (1994). The calculi of emergence: computation, dynamics and induction. Physica D: Nonlinear Phenomena, 75(1–3), 11–54. https://doi.org/10.1016/0167-2789(94)90273-9

Privacy Notice & Disclaimer:
This blog provides simplified educational science content, created with the assistance of both humans and AI. It may omit technical details, is provided “as is,” and does not collect personal data beyond basic anonymous analytics. For full details, please see our Privacy Notice and Disclaimer. Read About This Blog & Attribution Note for AI-Generated Content to know more about this blog project.

Test-Drive Your City: How Simple Simulations Make Smarter Policies

~ Manuel Castañón-Puga

Cities are messy. Many people, rules, and surprises collide, which means even good intentions can backfire. Sandoval Félix and Castañón-Puga argue that decision-makers should “mock up” policies on a computer first, like trying a route in a map app before leaving home. These lightweight models allow people to explore what might happen if they build a new park, change bus routes, or tighten zoning—before affecting the real city. That kind of “anticipatory knowledge” helps avoid short-term fixes that create long-term problems.

The chapter explains why this matters: cities aren’t machines that can be tuned with one knob. They’re complex systems where small tweaks can trigger big, unexpected outcomes, because everything is connected. In complex systems, patterns “emerge” from many small actions—think of traffic waves or shopping streets that pop up on their own. This is why looking only at one piece often fails. The complexity lens focuses on interactions and probabilities, rather than rigid plans, allowing policies to account for side effects across different parts of the city.

To explore these interactions, the authors highlight agent-based models—small worlds filled with “agents” (such as households, shops, or buses) that follow simple rules. There’s no central boss; each agent has limited knowledge and reacts to its surroundings. When you run the simulation, their choices add up to city-scale patterns. A related technique, cellular automata, applies these rules to a grid, allowing nearby cells to influence each other—useful because, in cities, what’s next door often matters most. These tools don’t predict the future with certainty, but they help identify counterintuitive moves, path-dependent traps, and situations where individual wins don’t add up to a public win.

Getting started is less scary if you treat it like learning a creative skill. The authors suggest tinkering first, building simple blocks, keeping version notes, and borrowing small code “snippets” from similar models. Even sketching a flow diagram helps you stay focused and avoid accidental behaviors. Then, present the results clearly: use plain language, visuals, and connect the outputs to real-life steps, such as which rules or budgets would need to be changed. Communication guides, such as ODD/ODD+ D and the STRESS checklist, can help keep your work organized and understandable for non-experts. The point isn’t perfection—it’s making choices that are better informed, more transparent, and less likely to surprise everyone later.

In everyday terms, this chapter is an invitation to play “what if?” with the city you care about. Treat models like a safe sandbox where you can test ideas fast and see the ripple effects, not a crystal ball. When you understand that cities are living networks, you’re more likely to ask better questions, spot side effects early, and push for policies that work in the real world—not just on paper.

Reference:
Félix, J. S., & Castañón-Puga, M. (2019). From simulation to implementation: Practical advice for policy makers who want to use computer modeling as an analysis and communication tool. In Studies in Systems, Decision and Control (Vol. 209). https://doi.org/10.1007/978-3-030-17985-4_6

Privacy Notice & Disclaimer:
This blog provides simplified educational science content, created with the assistance of both humans and AI. It may omit technical details, is provided “as is,” and does not collect personal data beyond basic anonymous analytics. For full details, please see our Privacy Notice and Disclaimer. Read About This Blog & Attribution Note for AI-Generated Content to know more about this blog project.