Imagine you’re sitting at your desk with a messy pile of LEGO bricks. You’re not trying to build anything specific. Still, every so often, pieces snap together in a way that unexpectedly resembles something recognizable—a tiny house, a creature, or a spaceship. Now, picture that instead of LEGO bricks, you have thousands of small molecules floating around on a particle or droplet somewhere on early Earth. According to Dyson, a similar process may have happened billions of years ago: random molecules bumping into each other until, by pure chance, some formed structures that helped create more structures like themselves.
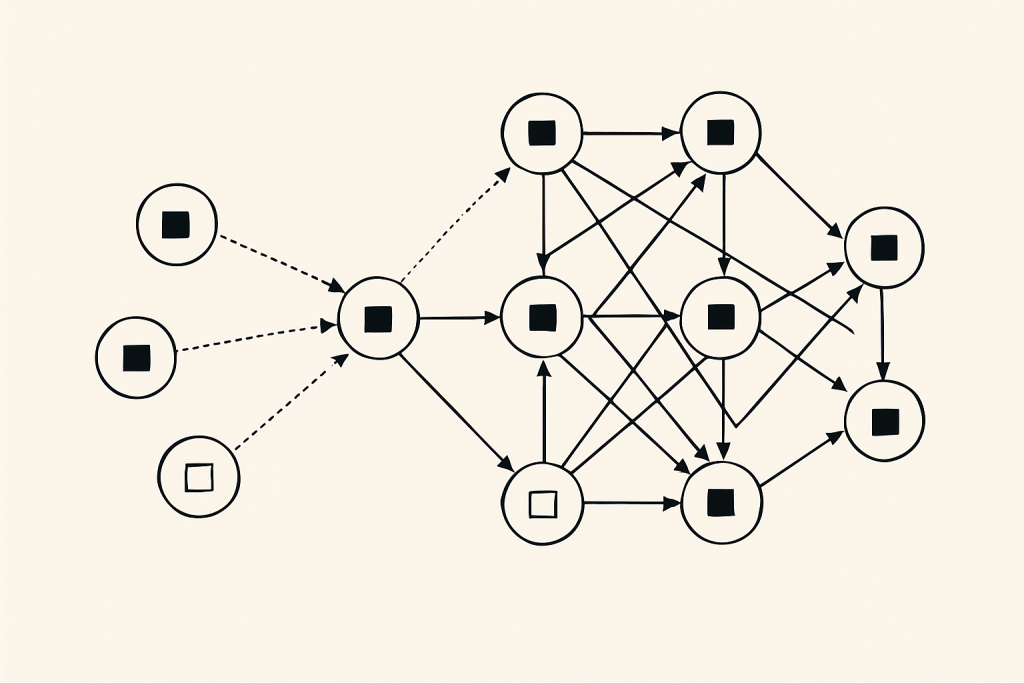
The idea Dyson describes is that life didn’t begin with a perfect genetic system, such as DNA, but with small ‘islands’ of molecules—clusters where a fixed number of monomers gathered and occasionally joined into tiny chains. Most of the time, these chains were useless, but every now and then, one of them would help another chain form. Dyson refers to those as ‘active’ monomers. When enough active ones appeared at once, a kind of order emerged: the molecules on the island became good at helping each other grow. To make this easier to imagine, think of a group of students working on a group project. If only one or two people are doing the work, not much happens. Still, if the group randomly ends up with several motivated people at the same time, suddenly the whole project becomes productive. Dyson’s model suggests that a similar team effect could have happened among primitive molecules.
Dyson’s calculations highlight that, even without natural selection, a small island of a few thousand monomers could have shifted from chaos to order through chance. Early life may have begun as a random event that stabilized once sufficient beneficial molecules accumulated. Dyson describes this early ‘ordered state’ as a messy mix of simple catalysts rather than modern cells. Once such an island became ordered, it could grow, absorb more material, and eventually split into two, making natural selection relevant only later. The main point is that significant changes in nature—and in life—often begin with small, unlikely steps that become possible when many small things come together.
Reflecting on your own life, Dyson’s model offers a simple lesson. Order doesn’t always come from careful planning; sometimes it emerges from many small attempts, even failed ones, that eventually align. Just as those early molecules needed luck and numerous small fluctuations to reach a stable, productive state, young people often require time and space to try, adjust their direction, and gradually form habits that support growth. What matters is staying in the game long enough for your ‘active pieces’—your motivation, interests, and skills-to come together. Once they align, progress feels natural instead of forced, much like how Dyson suggests early life first found its order.
Reference:
Dyson, F. J. (1982). A model for the origin of life. Journal of Molecular Evolution, 18(5), 344–350. https://doi.org/10.1007/BF01733901
Privacy Notice & Disclaimer:
This blog provides simplified educational science content, created with the assistance of both humans and AI. It may omit technical details, is provided “as is,” and does not collect personal data beyond basic anonymous analytics. For full details, please see our Privacy Notice and Disclaimer. Read About This Blog & Attribution Note for AI-Generated Content to know more about this blog project.